Optimale Steuerung
Die optimale Steuerung beschäftigt sich mit dem mathematischen Problem, ein durch Differentialgleichungen beschriebenes System so unter gegebenen Nebenbedingungen zu steuern, dass vorgegebene Zielkriterien optimiert werden. Praktische Anwendungen hierzu sind bspw. in den Bereichen Luft- und Raumfahrt, Industrial Engineering, Ökomomie, Biologie oder auch Medizin anzutreffen.
Wir beschäftigen uns mit Fragestellungen zur
- Diskretisierung und numerischen Lösung
- Regularisierung
- und Dualisierung
optimaler Steuerungsprobleme.
Anwendung: Optimale Steuerung eines optischen Sensors
Im Paper Optimal Control of an Optical System for Material Testing wird ein Prototyp für den automatische Test von Glasscheiben auf Materialfehler mit Hilfe eines optischen Sensors implementiert. Basierend auf einem nichtlinearen Optimierungsproblems wird eine numerische Methode zur optimalen Steuerung des Sensors in Echtzeit vorgestellt. Es stellt sich heraus, dass die optimale Steuerung in diesem Fall vom Typ bang-bang ist. Das heißt, der Sensor bewegt sich auf dem Förderband stets mit vollem Schub nach oben oder nach unten. Die folgende Abbildung zeigt an einem Beispiel einen einfach gesteuerten Sensor (rot) im Vergleich zum optimal gesteuerten Sensor (blau).
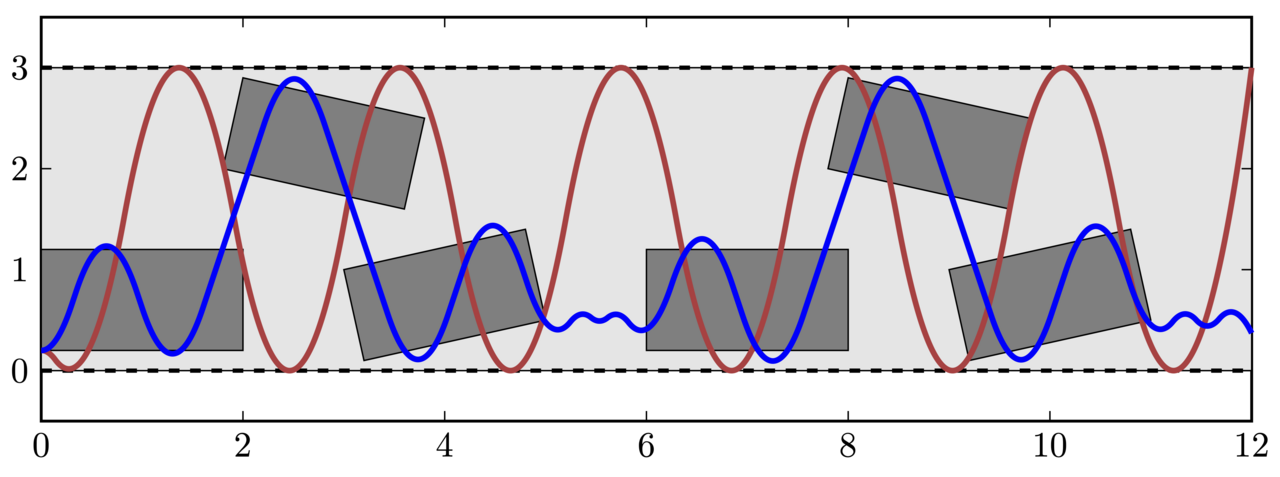
B. Martens und Ch. Schneider (2021)
Error Analysis for the Implicit Euler Discretization of Affine Optimal Control Problems with Index Two DAEs
Pure and Applied Functional Analysis, to appear
Ch. Schneider und G. Wachsmuth (2018)
Regularization and discretization error estimates for optimal control of ODEs with group sparsity
ESAIM: Control, Optimisation and Calculus of Variations 24(2), S. 811–834
https://doi.org/10.1051/cocv/2017049
W. Alt, Ch. Schneider und M. Seydenschwanz (2018)
Optimal Control of an Optical System for Material Testing
IFAC-PapersOnLine 51(2), S. 278–283
https://doi.org/10.1016/j.ifacol.2018.03.048
W. Alt, Ch. Schneider und M. Seydenschwanz (2016)
Regularization and implicit Euler discretization of linear-quadratic optimal control problems with bang-bang solutions
Applied Mathematics and Computation 287–288, S. 104–124
https://doi.org/10.1016/j.amc.2016.04.028
W. Alt, C. Y. Kaya und Ch. Schneider (2016)
Dualization and discretization of linear-quadratic control problems with bang-bang solutions
EURO Journal of Computational Optimization 4, S. 47–77
https://doi.org/10.1007/s13675-015-0049-4
W. Alt und Ch. Schneider (2015)
Linear-quadratic control problems with L¹-control cost
Optimal Control Applications and Methods 36(4), 2015, S. 512-534
https://doi.org/10.1002/oca.2126
Ch. Schneider and W. Alt (2014)
Regularization of Linear-Quadratic Control Problems with L¹-Control Cost
System Modeling and Optimization 443, S. 296–305
https://doi.org/10.1007/978-3-662-45504-3_29
W. Alt, Ch. Schneider und M. Seydenschwanz
EAGLE-Starthilfe Optimale Steuerung: Theorie und numerische Verfahren
Edition am Gutenbergplatz Leipzig, 2013, 117 S.
Vorwort, Inhaltsverzeichnis und Kap. 1, Homepage des Verlags
W. Alt, Ch. Schneider und M. Seydenschwanz
Ergänzungen zu EAGLE-Starthilfe Optimale Steuerung: Theorie und numerische Verfahren
Link zur PDF-Version


